一个线性规划有以下的基本形式, 即均是等式约束.
\begin{array}{ll}\min & c_1x_1 + … + c_n x_n\\ \text{s.t.} & a_{11}x_1 + … + a_{1n}x_n= b_1\\ &a_{21}x_1 +…+ a_{2n}x_n = b_2 \\ &\qquad \vdots \\ &a_{m1}x_1 +…+ a_{mn}x_n = b_m \end{array}
其中 $x_j \ge 0, j=1,…,n$, $b_i \ge 0,i =1,…,m$
设 $$A = \begin{pmatrix}a_{11}&a_{12}&\dots&a_{1n}\\ a_{21}& a_{22}&\dots & a_{2n}\\ \vdots & \vdots & &\vdots \\ a_{m1}&a_{m2}&\dots &a_{mn}\end{pmatrix},B = \begin{pmatrix}b_1\\b_2\\ \vdots \\ b_m\end{pmatrix}$$
找到 $A$ 中的 $m$ 个线性无关的列向量, 构成一个新矩阵 $P$. 将 $AX=B$ 两边用 $P^{-1}$ 去乘, 得到 $$P^{-1}A X = P^{-1}B$$
开始使用表格来处理
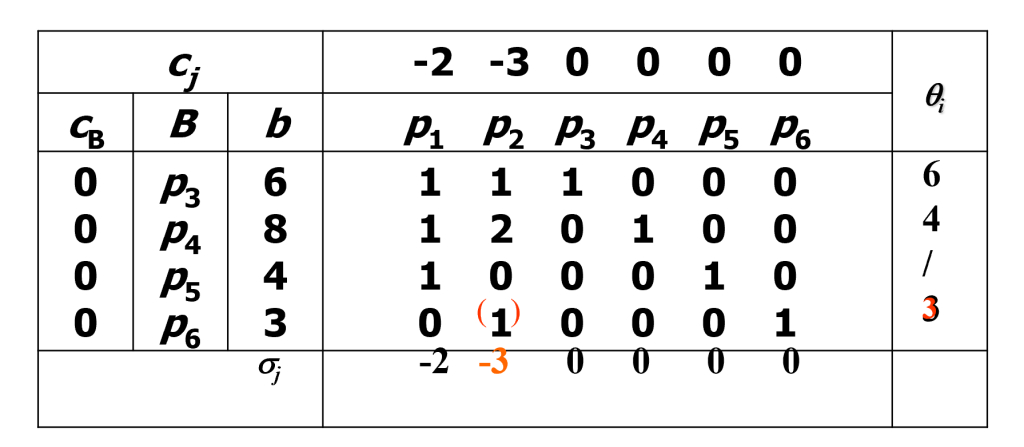
以该表格为例, 我们来研究怎么计算 $\sigma_j$ 和 $\theta_i$
$$\sigma_j = c_j – c_B \cdot p_j \quad \text{这里的 $c_B,p_j$ 指一列向量, $c_j$ 指单个元素 }$$
其中 $\cdot$ 为内积运算. $\sigma_j$ 只需要计算那些没被选为基向量的列, 如果 $\sigma_j$ 全都大于等 $0$, 那就说明我们已经得到了最优的基向量. 只需要求解基向量构成矩阵 $P$, $PX = B$ 的解, 再改写成原方程的解. (其余列对应的变量置 $0$)
接下来研究如果 $\sigma_j$ 中还有负数, 找到最小的那一列 $p_k$, 它将被加入到基向量中, 现在确定要去掉哪个基向量. 通过 $\theta_i$ 来决定.
$$\theta = \frac{b}{p}\quad \text{$b,p$两个列向量对应分量相除, 需要 $p$ 中元素$>0$ 才计算}$$
寻找 $\theta_i$ 中的最小的那一行对应的 $p_i$. 它作为出基向量. 重复上述的做法, 直到找到合适的基向量.